Introduction
Traditional volatility trades used to involve buying and selling portfolios of call and put options, straddles or strangles, and then possibly delta-hedging these positions. But such volatility positions were not pure and this led to a search for volatility tools whose payoff function would depend on volatility risk only. In this part we are going to see two volatility instruments that were developed : Volatility and variance swaps.
Variance is the second centered moment of a random variable. Volatility instruments require convexity adjustments, whereas variance instruments in general do not. When we talk about vega, for example , we refer to variance vega. This is the sensitivity of the option’s price with respect to sigma^2 not sigma.
Volatility Positions
Volatility positions can be taken for the purpose of hedging a volatility exposure or speculating on the future behavior of volatility.
Volatility Trading Using Options
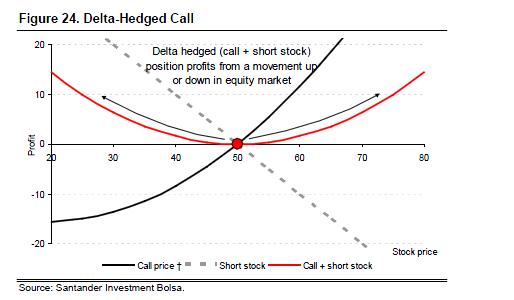
While directional investors typically use options for their equity exposure, volatility investors delta hedge their equity exposure. A delta-hedged option (call or put) is not exposed to equity markets, but only to volatility markets. We demonstrate how volatility investors are exposed to dividend and borrow cost risk and how volatility traders can ‘pin’ a stock approaching expiry.
VOL TRADING VIA CALLS AND PUTS IS IDENTICAL (PUT-CALL PARITY)
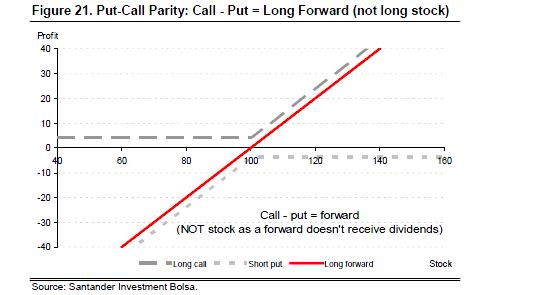
A forward is a contract that obliges the investor to buy (or sell if you have sold the forward) a security on a certain expiry date (but not before) at a certain strike price. A portfolio of a long European call and a short European put of identical expiry and strike is the same as a forward of that expiry and strike, as shown in Figure 21. This means that if a call, a put or a straddle is delta hedged with a forward contract (not stock), the end profile is identical. We note put-call parity is only true for European options, as American options can be exercised before expiry (although in practice they seldom are).
Delta hedging must be done with forward of identical maturity for put call parity
It is important to note that the delta hedging must be done with a forward of identical maturity to the options. If it is done with a different maturity, or with stock, there will be dividend risk. This is because a forward, like a European call or put, gives the right to a security at maturity but does not give the right to any benefits such as dividends that have an ex date before expiry. A long forward position is therefore equal to long stock and short dividends that go ex before maturity (assuming interest rates and borrow cost are zero or are hedged). This can be seen from the diagram below, as a stock will fall by the value of the dividend (subject to a suitable tax rate) on the ex date. The dividend risk of an option is therefore equal to the delta.
DELTA HEDGING AN OPTION REMOVES EQUITY RISK
Delta-hedged option gives a position whose profitability is determined by volatility
If an option is purchased at an implied volatility that is lower than the realised volatility over the life of the option, then the investor, in theory, earns a profit from buying cheap volatility. However, the effect of buying cheap volatility is dwarfed by the profit or loss from the direction of the equity market. For this reason, directional investors are usually more concerned with premium rather than implied volatility. Volatility investors will, however, hedge the equity exposure. This will result in a position whose profitability is solely determined by the volatility (not direction) of the underlying. As delta measures the equity sensitivity of an option, removing equity exposure is called delta hedging (as a portfolio with no equity exposure has delta = 0).
Delta hedging example
As the delta of a portfolio is equal to the sum of the deltas of the securities in the portfolio, a position can be delta hedged by purchasing, or going short, a number of shares (or futures in the case of an index) equal to the delta. For example, if ten call options have been bought with a delta of 40%, then four shares (10 × 40% = 4) have to be shorted to create a portfolio of zero delta. The shares have to be shorted as a call option has positive delta; hence, the delta hedge has to be negative for the sum of the two positions to have zero delta. If we were long a put (which has negative delta), then we would have to buy stock to ensure the overall delta was zero.
Constant delta hedging is called gamma scalping
The rate delta changes as spot moves is called gamma; hence, gamma is the convexity of the payout. As the delta changes, a volatility investor has to delta hedge in order to ensure there is no equity exposure. Constantly delta hedging in this way is called gamma scalping, as it ensures a long volatility position earns a profit as spot moves.
Delta-hedged option gives a position whose profitability is determined by volatility
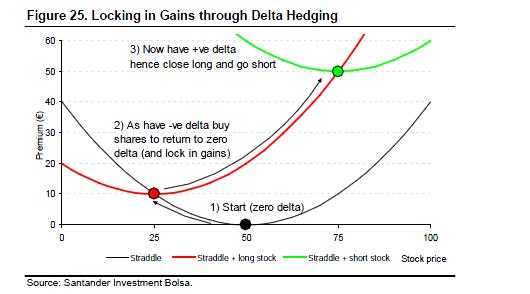
Gamma scalping (delta re-hedging) locks in profit as underlying moves
We shall assume an investor has purchased a zero delta straddle (or strangle), but the argument will hold for long call or put positions as well. If equity markets fall (from position 1 to position 2 in the chart) the position will become profitable and the delta will decrease from zero to a negative value. In order to lock in the profit, the investor must buy stock (or futures) for the portfolio to return to zero delta. Now that the portfolio is equity market neutral, it will profit from a movement up or down in the equity market. If equity markets then rise, the initial profit will be kept and a further profit earned (movement from position 2 to position 3). At position 3 the stock (or futures) position is sold and a short position initiated to return the position to zero delta.
OPTION TRADING RULES OF THUMB
To calculate option premiums and volatility exactly is typically too difficult to do without the aid of a tool. However, there are some useful rules of thumb that can be used to give an estimate. These are a useful sanity check in case an input to a pricing model has been entered incorrectly.
- Profit from delta hedging is proportional to square of return. Due to the convexity of an option, if the volatility is doubled the profits from delta hedging are multiplied by a factor of four. For this reason, variance (which looks at squared returns) is a better measure of deviation than volatility.
- ATM option premium in percent is roughly 0.4 × volatility × square root of time. If one assumes zero interest rates and dividends, then the formula for the premium of an ATM call or put option simplifies to 0.4 × σ × √T. Therefore, a one-year ATM option on an underlying with 20% implied is worth c8% (= 0.4 × 20% × √1). OTM options can be calculated from this estimate using an estimated 50% delta.
- Historical annualised volatility roughly equal to 16 × percentage daily move. Historical volatility can be estimated by multiplying the typical return over a period by the square root of the number of periods in a year (eg, 52 weeks or 12 months in a year). Hence, if a security moves 1% a day, it has an annualised volatility of 16% (as 16 ≈ √252 and we assume there are 252 trading days).
Historically, annualised volatility is roughly equal to 16 × percentage daily move
A stock that moves 1% a day has 16% volatility, and a stock that moves 2% has 32% volatility
As returns are normally close to 1 (=100%) the log of returns is very similar to ‘return – 1’ (which is the percentage change of the price). Hence, to calculate the annualised volatility for a given percentage move, all that is needed is to annualise the percentage change in the price. This is done by multiplying the percentage move by the square root of the number of samples in a year (as volatility is the square root of variance). For example, market convention is to assume there are approximately 252 trading days a year. If a stock moves 1% a day, then its volatility is 1% × √252, which is approximately 1% × 16 = 16% volatility. Similarly, if a stock moves 2% a day it has 32% volatility.
- Number of trading days in year = 252 => Multiply daily returns by √252 ≈ 16
- Number of weeks in year = 52 => Multiply weekly returns by √52 ≈ 7
- Number of months in year = 12 => Multiply monthly returns by √12 ≈ 3.5
ATM option premium in percent is roughly 0.4 × volatility × square root of time
Call price = S N(d1) – K N(d2) e-rT
Assuming zero interest rates and dividends (r = 0)
ATM call price = S N(σ × √T / 2) – S N(-σ × √T / 2) as K=S (as ATM)
ATM call price = S × σ × √T / √(2π)
ATM call price = σ × √T / √(2π) in percent
ATM call price ≈ 0.4 × σ × √T in percent
where:
Definition of d1 and d2 is the standard Black-Scholes formula.
σ = implied volatility
S = spot
K = strike
R = interest rate
T = time to expiry
N(z) = cumulative normal distribution
Example 1
1Y ATM option on an underlying with 20% implied is worth c.8% (=0.4 × 20% × √1)
Example 2
3M ATM option on an underlying with 20% implied is worth c.4% (=0.4 × 20% × √0.25 =0.4 × 20% × 0.5)
OTM options can be calculated by assuming 50% delta
If an index is 3000pts and has a 20% implied then the price of a 3M ATM option is approximately 240pts (3000×8% as calculated above). A 3200 call is therefore approximately 240 – 50% (3200-3000) = 140pts assuming a 50% delta. Similarly, a 3200 put is approximately 340pts.
Profit from delta hedging is proportional to percentage move squared
Due to the convexity of an option, if the volatility is doubled, the profits from delta hedging are multiplied by a factor of four. For this reason, variance (which looks at squared returns) is a better measure of deviation than volatility. Assuming constant volatility, zero interest rates and dividend, the daily profit and loss (P&L) from delta hedging an option is given below.
Daily P&L from option = Delta P&L + Gamma P&L + Theta P&L
Daily P&L from option = Sδ + S2γ /2 + tθ where S is change in Stock and t is time
Daily P&L from option – Sδ = + S2γ /2 + tθ = Delta hedged P&L from option
Delta hedged P&L from option = S2γ /2 + cost term (tθ does not depend on stock price)
where:
δ = delta
γ = gamma
t = time
θ = theta
Hedge investors prefer occasional large moves to constant small moves
If the effect of theta is ignored (as it is a cost that does not depend on the size of the stock price movement), the profit of a delta hedged option position is equal to a scaling factor (gamma/2) multiplied by the square of the return. This means that the profit from a 2% move in a stock price is four times (22=4) the profit from a 1% move in stock price.
This can also be seen from Figure 27 below, as the additional profit from the move from 1% to 2% is three times the profit from 0% to 1% (for a total profit four times the profit for a 1% move).
Example: make same delta hedge profit with 1% a day move as 2% every four days
Let’s assume there are two stocks: one of them moves 1% a day and the other 2% every four days (see Figure 28 below). Both stocks have the same 16% volatility and delta hedging them earns the same profit (as four times as much profit is earned on the days the stock moves 2% as when it moves 1%).
VARIANCE IS THE KEY, NOT VOLATILITY
Partly due to its use in Black-Scholes, historically, volatility has been used as the measure of deviation for financial assets. However, the correct measure of deviation is variance (or volatility squared). Volatility should be considered to be a derivative of variance. The realisation that variance should be used instead of volatility led volatility indices, such as the VIX, to move away from ATM volatility (VXO index) towards a variance-based calculation.
VARIANCE, NOT VOLATILITY, IS CORRECT MEASURE FOR DEVIATION
There are three reasons why variance, not volatility, should be used as the correct measure for volatility. However, despite these reasons, even variance swaps are normally quoted as the square root of variance for an easier comparison with the implied volatility of options (but we note that skew and convexity mean the fair price of variance should always trade above ATM options).
Variance takes into account implied volatility at all stock prices. Variance takes into account the implied volatility of all strikes with the same expiry (while ATM implied will change with spot, even if volatility surface does not change).
Deviations need to be squared to avoid cancelling. Mathematically, if deviations were simply summed then positive and negative deviations would cancel. This is why the sum of squared deviations is taken (variance) to prevent the deviations from cancelling. Taking the square root of this sum (volatility) should be considered a derivative of this pure measure of deviation (variance).
Profit from a delta-hedged option depends on the square of the return. Due to the convexity of an option, if the volatility is doubled, the profits from delta hedging are multiplied by a factor of four. For this reason, variance (which looks at squared returns) is a better measure of deviation than volatility.
1/VARIANCE TAKES INTO ACCOUNT VOLATILITY AT ALL STOCK PRICES
When looking at how rich or cheap options with the same maturity are, rather than looking at the implied volatility for a certain strike (ie, ATM or another suitable strike) it is better to look at the implied variance as it takes into account the implied volatility of all strikes. For example, if an option with a fixed strike that is initially ATM is bought, then as soon as spot moves it is no longer ATM. However, if a variance swap (or log contract4
4 For more details, see the section Volatility, Variance and Gamma Swaps. of options in the absence of a variance swap market) is bought, then its traded level is applicable no matter what the level of spot. The fact a variance swap (or log contract) payout depends only on the realised variance and is not path dependent makes it the ideal measure for deviation.
2/DEVIATIONS NEED TO BE SQUARED TO AVOID CANCELLING
If a seesaw has two weights on it and the weights are the same distance either side from the pivot, the weights are balanced as the centre of the mass is in line with the pivot (see graph on left hand side below). If the weights are further away from the pivot the centre of the mass (hence the average/expected distance of the weights) is still in line with the pivot (see graph on right hand side below). If the deviation of the two weights from the pivot is summed together, in both cases they would be zero (as one weight’s deviation from the pivot is the negative of the other). In order to avoid the deviation cancelling this way, the square of the deviation (or variance) is taken, as the square of a number is always positive.
3 PROFIT FROM DELTA HEDGING PROPORTIONAL TO RETURN SQUARED
Assuming constant volatility, zero interest rates and dividend, the daily profit and loss (P&L) from delta hedging an option is given below:
Delta-hedged P&L from option = S2γ /2 + cost term
where:
γ = gamma
This can also be seen from Figure 27 Profile of a Delta-Hedged Option in the previous section (page 45), as the additional profit from the move from 1% to 2% is three times the profit from 0% to 1% (for a total profit four times the profit for a 1% move).
SOURCE :
- Santander Investment Bolsa.
- Principales of Financial Engineering, Salih N. Neftci